Vaughan Jones

Flatland, a great place to do algebra

Monday, April 11, 2011

7-8:00PM

Filene Auditorium, Moore Hall

Abstract: Edwin Abbott, an English non-mathematician of the Victorian era, wrote a book called "Flatland" about life in a two dimensional world, and its hero's travels to other dimensions. I will use this dimensional voyage to relate one of my own which will go from one dimension to infinitely many, then settle solidly in two dimensions. The quantum world in two dimensions is even more bizarre than in three dimensions and the algebra we will encounter is being used in an attempt to build a quantum computer based on these very peculiarities.

Note: This talk will be accessible to undergraduates.

NB: A PDF version of this announcement (suitable for posting) is also available.

The Onset of Wildness

Monday, April 11, 2011

4-5:00PM

008 Kemeny Hall

Abstract: There are many instances in mathematics of some phenomenon, depending on a parameter, which is well behaved for a while but at a certain value of the parameter, becomes wild. The onset of turbulence is a well known example but there are examples in algebra such as Gabriel's quiver theory.

Subfactors are objects that, among other things, extend the notion of finite groups, their representations and permutation actions. The "size" of a subfactor is measured by a number called its index and one might expect an onset of wildness phenomenon as the index grows. Indeed since the mid 1980's it has been known that there is an A-D-E Coxeter graph classification of subfactors of index less than or equal to four. But Bisch and Haagerup showed that at index 6 the situation is "wild". This is because free product of Z/2Z and Z/3Z is almost a free group. But in subfactor land there is a subfactor of index approximately 2.6 so it is possible that wildness begins at about 5.2. There is thus a hope of a complete enumeration of subfactors between index 4 and 5.2. This enumeration begins with Haagerup's subfactor of index 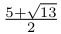and other exotic objects whose existence is only known by combinatorial and planar methods.

Random matrices, von Neumann algebras and (2+1)-dimensional topological quantum field theories.

Tuesday, April 12, 2011

4-5:00PM

008 Kemeny Hall

Abstract: Voiculescu used the large N limit of random matrices to define a trace on the algebra of noncommutative polynomials. A few years ago, Guionnet, Shlyakhetnko and I discovered how to extend the Voiculescu trace to more general graded algebras coming from planar algebras. These (non-commutative) graded algebras have a formal resemblance to the canonical ring of an algebraic variety. Among the constructions arising in this work was a notion of matrix model where the number of matrices is non integral. Planar ideas lead to the consideration of potentials in matrix models which allow enumeration of various planar structures. In more recent work Curran and Shlyakhtenko have used the ideas to give a “visible” construction of the quantum double of a subfactor.